Search

Les Matrices

 

Moyen

  1. Le concept
  2. La convention
  3. La manipulation
    1. Créer une matrice
    2. Accéder à une cellule d'une matrice
    3. Parcourir une matrice

Le concept

Les matrices sont des listes à 2 dimensions, c'est-à-dire une liste dans une liste.

La convention

Voici à quoi ressemble une matrice.

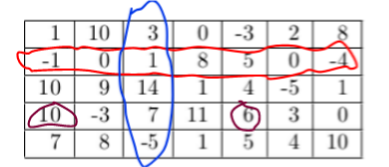
Matrice

  1. Les cercles violets sont des "cellules".
  2. Le cercle horizontal est une "ligne"(row en anglais) dénoté n.
  3. Le cercle vertical est une "colonne"(column en anglais) dénoté m.
  4. Cette matrice est de taille 5x7 (row x col) .
  5. La première ligne ( resp. colonne ) est 0 et la dernière ligne (resp. colonne) est n-1 (resp m-1).
      6. - Dans le cas d'un 5x7, la première ligne (resp. colonne) est 0 et la dernière ligne (resp. colonne) est 5-1 = 4 (resp 7-1 = 6).

La manipulation

Nous allons voir comment:
  1. Créer une matrice.
  2. Accéder à une cellule d'une matrice.
  3. Parcourir une matrice.

Créer une matrice

Créeons une matrice de taille 5x4 remplie de 0. 
from algopy import matrix #Cela nous permet d'afficher les matrices plus joliment.

M = [] #Liste principale.
subL = [0, 0, 0, 0] #sous-liste avec 4 zéros.

for i in range(5):
    M.append(subL) #On ajoute la liste "subL" dans la liste principale "M".

matrix.prettyprint(M)

>>>
-----------------
| 0 | 0 | 0 | 0 |
-----------------
| 0 | 0 | 0 | 0 |
-----------------
| 0 | 0 | 0 | 0 |
-----------------
| 0 | 0 | 0 | 0 |
-----------------
| 0 | 0 | 0 | 0 |
-----------------
Voici une autre manière de créer une matrice 5x4. Cette fois-ci, on l'a remplira avec des valeurs aléatoires. 
from algopy import matrix #Cela nous permet d'afficher les matrices plus joliment.
from random import randint

n = 5
m = 4

M = []
for row in range(n):
    subL = []
    for col in range(m):
        subL.append(randint(0,10))
    M.append(subL) #On ajoute la liste "subL" dans la liste principale "M".
    
matrix.prettyprint(M)

>>>
---------------------
|  5 |  9 |  1 |  0 |
---------------------
|  6 |  4 |  0 |  1 |
---------------------
|  1 |  2 |  7 |  3 |
---------------------
|  7 |  4 |  2 |  6 |
---------------------
|  2 | 10 |  7 |  4 |
---------------------

Accéder à une cellule d'une matrice

La syntaxe pour accéder à une cellule: M[row][col] 
M[0][0] #Cellule de la ligne 1 & colonne 1.

>>> 5



M[0][1] #Cellule de la ligne 1 & colonne 2.

>>> 9



M[4][3] #Cellule de la ligne 4 & colonne 3.

>>> 4

Parcourir une matrice 

for row in range(n):
    for col in range(m):
        print(M[row][col], end = "|")
    print() #Retour à la ligne

>>>
5|9|1|0|
6|4|0|1|
1|2|7|3|
7|4|2|6|
2|10|7|4|

Pour résumer:

- Les matrices sont des listes de dimensions 2, c'est-à-dire une liste dans une liste.
- D'après l'image précédente:
      - Les cercles violets sont des "cellules".
      - Le cercle horizontal est une "ligne"(row en anglais) dénoté n.
      - Le cercle vertical est une "colonne"(column en anglais) dénoté m.
      - Cette matrice est de taille 5x7 (row x col) .
      - La première ligne ( resp. colonne ) est 0 et la dernière ligne (resp. colonne) est n-1 (resp m-1).
      - Dans le cas d'un 5x7, la première ligne (resp. colonne) est 0 et la dernière ligne (resp. colonne) est 5-1       = 4 (resp 7-1 = 6).

- Nous avons vu comment:
       Créer une matrice.
       Accéder à une cellule d'une matrice.
       Parcourir une matrice.